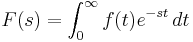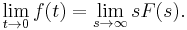Initial value theorem

In mathematical analysis, the initial value theorem is a theorem used to relate frequency domain expressions to the time domain behavior as time approaches zero.[1]

Let

F(s) = \int_0^\infty f(t) e^{-st}\,dt

be the (one-sided) Laplace transform of ƒ(t). The initial value theorem then says[2]

\lim_{t\to 0}f(t)=\lim_{s\to\infty}{sF(s)}. \,

See also

Notes

  1. ^ http://fourier.eng.hmc.edu/e102/lectures/Laplace_Transform/node17.html
  2. ^ Robert H. Cannon, Dynamics of Physical Systems, Courier Dover Publications, 2003, page 567.